可汗学院的教程:https://www.khanacademy.org/math/multivariable-calculus,这是目前找到最好的教程,有视频、文本和练习,学习曲线非常平缓。(AP是面向高中生的,讲得会不够深入。MIT开放出来的视频是几十年的,质量太差,看着难受。网易公开课里清华的废话比较多,东西比较旧。可汗学院的鼠标视频看着也是很难受的,像素太低,等号大于号有时都分不清。)
矢量与矩阵(vectors and matrics)
点乘(dot product)就像是计算合力,点乘的结果是标量。
叉乘(cross product)的方向要用右手定则,值是面积。有点像计算电磁感应。叉乘的结果是矢量。叉乘只适用于三维矢量。
行列式(determinant)这个名词的翻译不是特别直观,它反映了坐标经过一系列转换后的一个缩放系数,绝对值大于1是放大了,小于1是缩小了,负数表示坐标翻转了。
行列式和叉乘的关系如下:

偏微分和梯度(Partial derivative and gradient)
magnitude:暂时翻译为长度,用两层绝对值符号表示,是向量各分量值的平方和再开方。
梯度可以写成倒三角形,也可以写成grad。倒三角形符号本身叫nabla。
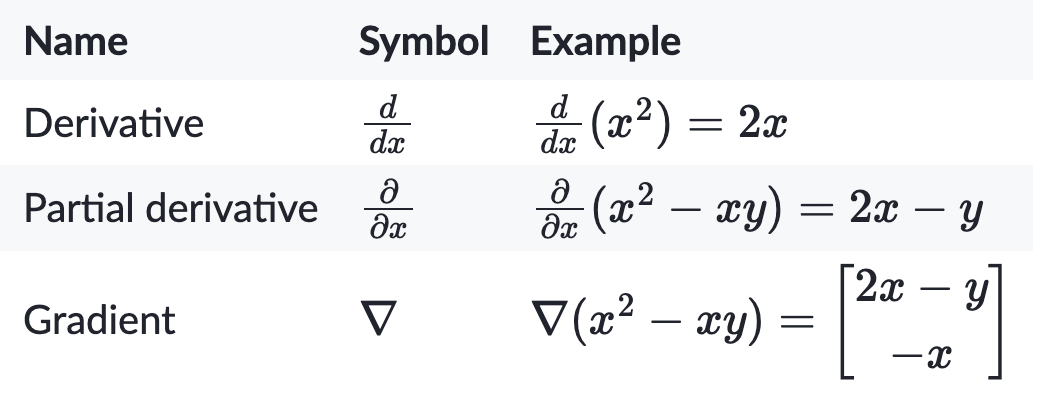
This symbol
方向导数(Directional derivatives):偏导向量“点乘”方向单位向量,得到一个标量,物理意义是该方向上的坡度。
曲率(curvature,K)
radius of curvature: 曲率半径R
K=1/R
曲率半径越大,曲率越小,越接近直线。
helix:螺旋状物
散度(Divergence)
大于0时表示向外流出,小于0时表示向内流进。散度值等于各方向偏导相加。
div(F) = ▽·F,输入是一个矢量,输出果是一个标量。注意,这里是点乘它和grad(F)是不同的。

旋度(curl)
二维的旋度2d-curl(F) = ▽xF,输入是一个矢量,输出是一个标量。逆时针为正,顺时针为负。值的大小表示旋转速度(弧度/秒)。
三维的旋度是一个矢量。三维旋度的方向是右手定则拇指指向方向,大小(行列式)表示旋转速度的两倍(因为它是值上下两个方向旋转速度相加的结果)。
拉普拉斯算子(Laplacian)
△f = ▽·▽f(div点乘grad(f),f的梯度的散度,是一个标量),是f对各坐标分量的二次导数相加。山谷大于0,山峰小于0。其它地方的值含义暂不清楚。
调和函数(hamonic function)
拉普拉斯算子恒为0的函数。一种没有山峰或山谷的函数。例如一维函数中的线性函数。
雅可比矩阵(Jacobian)
用于坐标变换。对于二维雅可比行列式,其值可以认为是图形在坐标系转换后面积的变化比例。


Hessian matrix
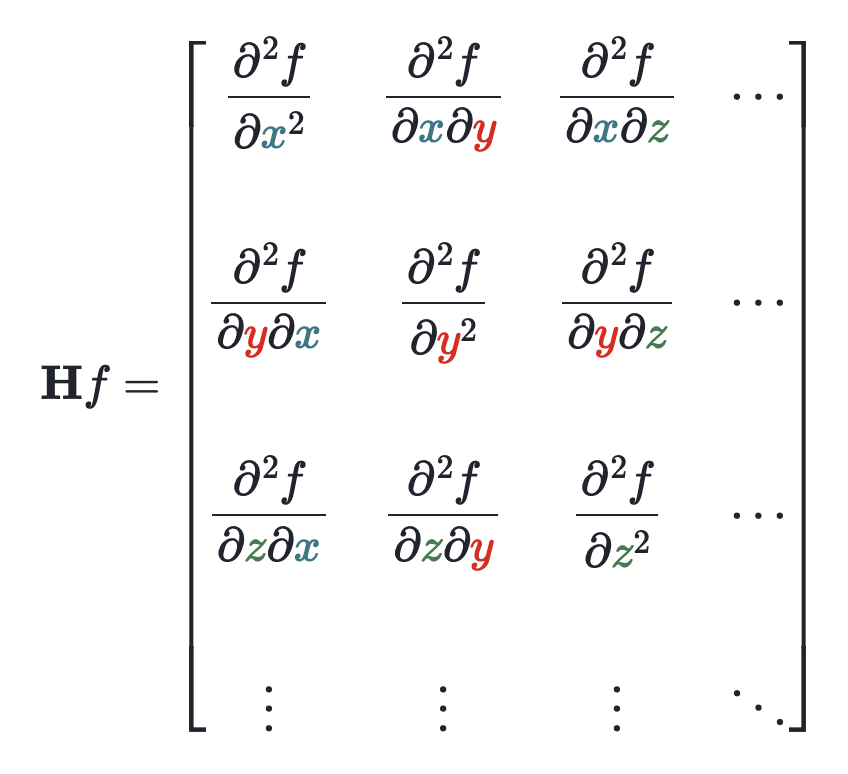
二次近似(Quadratic approximation)
梯度场(Gradient Field)
梯度场(Gradient Field)是由数量场得到的矢量场。
具体来说,如果一个多变量函数f(x1,x2,...,xn)在每个点上都有定义,并且其偏导数存在,那么该函数的梯度∇f就是一个矢量场,即梯度场。梯度场中的每个矢量都指向函数值增长最快的方向,其大小为该方向上的方向导数的最大值。
此外,梯度场的一个重要性质是其线积分与积分路径无关,只与始末位置在势函数中的值有关。这一性质类比重力场和电场,使得梯度场在物理学、工程学等领域有着广泛的应用。例如,在物理学中,梯度常用于描述电场、磁场、温度场等的分布和变化;在工程学中,梯度则可能用于优化问题,如寻找函数的最值点。
保守矢量场(Conservative Vector Field)
保守矢量场路径无关、无旋。
如果重力场不是保守矢量场就会出现下图的情况:

单位法向量(unit normal vector)
是一个与曲线或曲面垂直的向量,并且其长度(模)为 1。
Simple, Closed, Piecewise-smooth, Connected
A curve is simple if it never crosses itself, closed if it starts and ends in the same place, and piecewise-smooth if can be broken up into a finite number of smooth parts. (Smooth means differentiable.)
A region is simply connected if it never intersects itself and it has no holes.
格林定理(Green's Theorem)

换句话说,格林定理指出旋度(公式里的区域积分部分就是旋度公式)等于对区域边界做线积分,这是非常符合旋度物理意义的直觉的。
作为对比,下面是散度定理:

斯托克斯定理(Stokes' theorem)
- Green theorem:主要应用于二维平面区域,处理平面上的曲线积分和二重积分之间的转换问题,例如在计算平面向量场沿闭曲线的环量以及平面区域上的通量等问题中经常用到。
- Stokes' theorem:应用于三维空间,用于处理三维向量场中曲面的面积分与边界曲线的线积分之间的关系,在分析三维空间中的电磁学问题、流体涡旋等方面有广泛应用。
- Green theorem:从几何上看,它可以理解为平面区域\(D\)上的某种 “净流量”(由\(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\)表示)与沿着区域\(D\)的边界曲线\(L\)的 “流量” 之间的关系。
- Stokes' theorem:其几何意义是向量场沿闭曲线\(C\)的环量等于该向量场的旋度在以\(C\)为边界的曲面\(S\)上的通量,直观地体现了曲面上的 “旋转” 情况与边界曲线的 “环量” 之间的联系。

极值判断方法


评论1
感谢分享
很有用,感谢分享